개요
데이터베이스에 대한 기술 면접 준비를 하다가 B-Tree, B+Tree가 이진 탐색 트리의 단점을 보완하기 위해 개발되었다는 걸 봤다.
B-Tree, B+Tree를 이해하기 위해선 우선 이진 탐색 트리를 알고 있어야 더 쉽게 이해할 수 있을 것 같아서 정리하게 되었다.
이진 탐색 트리

이진 탐색 트리는 각 노드가 최대 두 개의 자식을 가지며, 왼쪽 자식에는 부모 노드보다 작은 값이, 오른쪽 자식에는 부모 노드보다 큰 값이 저장되는 트리 구조이다.
이러한 구조가 모든 노드에 적용되기 때문에 항상 정렬된 상태를 유지할 수 있다.
이렇게 정렬된 트리에서 찾고자 하는 노드를 탐색할 땐 Up-Down을 진행하며, 노드들의 수를 줄여가며 찾을 수 있다.
만약 이진 탐색 트리에 100개의 노드가 있다면 최적의 경우엔 6, 7개의 노드를 탐색하면 원하는 노드를 찾을 수 있을 것이다.
최악의 경우는 삽입되는 노드들이 정렬되어 있는 경우이다.
만약 1, 2, 3, 4, 5 노드들이 삽입될 경우를 생각해보자.
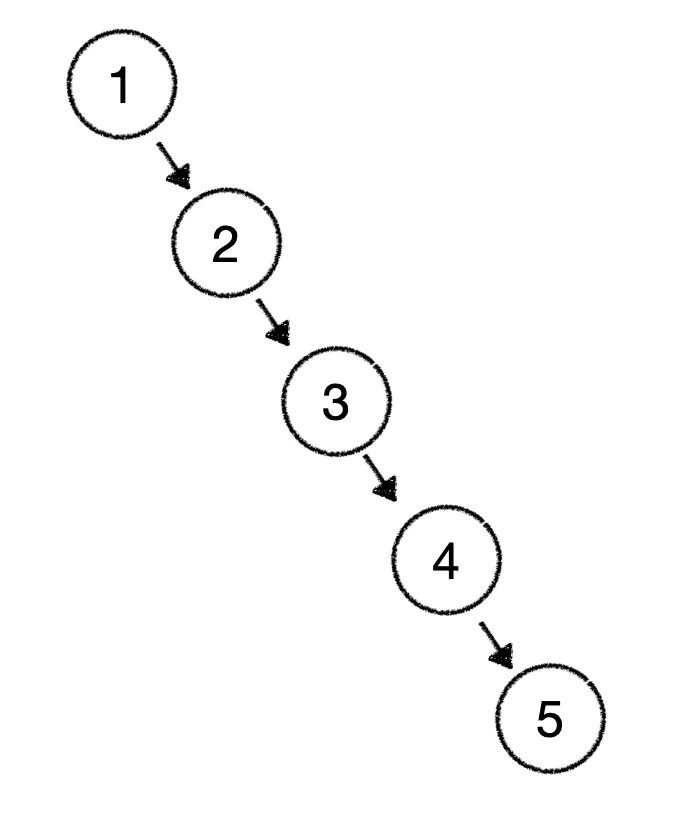
위의 이미지처럼 정렬된 노드들이 삽입된다면, 계속해서 오른쪽 서브 트리에 노드가 삽입될 것이다.
이럴 경우엔 만약 5 노드를 찾기 위해선 총 5개의 노드를 탐색해야 한다.
시간 복잡도가 O(N)인 것이다.
삽입 연산
이진 탐색 트리에서 삽입은 어느 곳에 노드를 넣을 시 결정하는 탐색을 먼저 수행해야 한다.
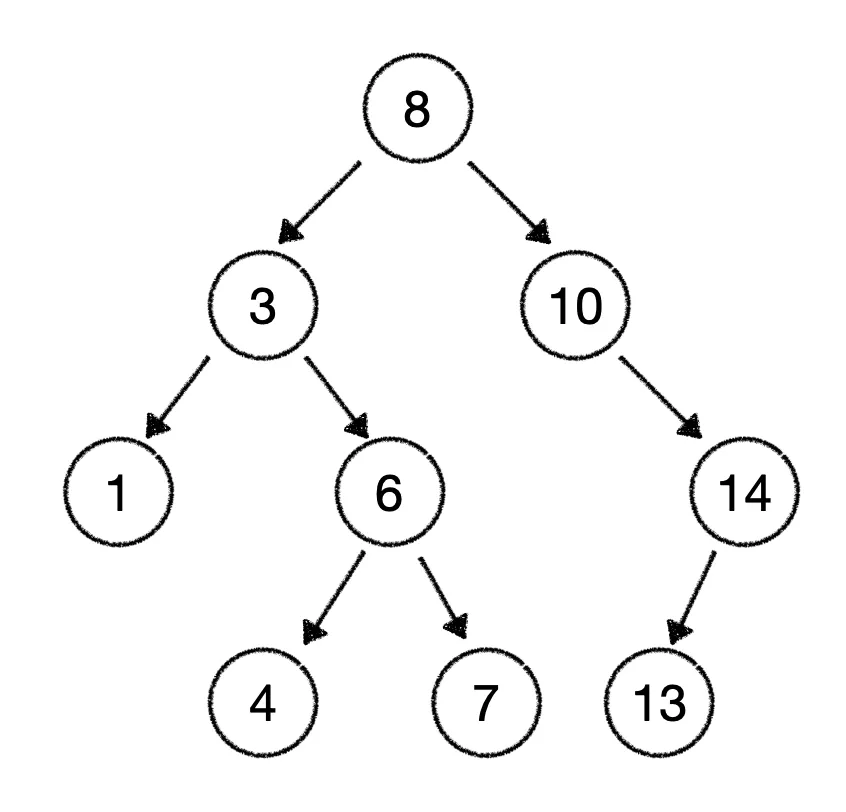
위의 트리에서 만약 9를 삽입하고자 할 때, 일단 삽입할 공간을 탐색한다.
왜냐하면 삽입하고자 하는 노드가 이미 존재한다면, 노드를 삽입할 수 없기 때문이다. (참고로 이진 탐색 트리 내부의 노드는 중복이 있으면 안 됨!)

삽입은 비교적 간단하다.
삭제 연산
삭제 연산은 탐색, 삽입 연산보다 좀 까다롭다.
그 이유는 정렬된 상태를 유지하려는 이진 탐색 트리의 성질 때문이다.
일단 삭제 연산의 경우의 수는 총 2가지가 있다.
- 자식이 없는 노드를 삭제하는 경우
- 자식이 있는 있는 노드를 삭제하는 경우
자식이 없는 노드를 삭제하는 경우
가장 간단한 경우이다.
리프 노드(자식이 없는 노드)는 자식이 없기 때문에 그냥 삭제하면 된다.
아래 이미지는 트리에서 13을 삭제하고자 하는 경우이다.

13 노드의 위치를 찾았다면 그냥 삭제한다.

결과는 위의 이미지와 같다.
후계자 노드
자식이 없는 노드는 후계자 노드가 필요 없지만, 자식이 하나라도 있는 경우엔 후계자 노드가 필요하다.
그 이유는 한 노드가 삭제되었다고 자식 노드들까지 삭제되면 안 되기 때문이다.
그렇기 때문에 삭제된 노드를 대체할 후계자 노드가 삭제된 노드의 위치로 이동한다.
후계자 노드를 정하는 기준은 다음과 같다.
- 왼쪽 서브트리에서 가장 큰 노드
- 오른쪽 서브트리에서 가장 작은 노드
이렇게 기준을 정한 이유는 이진 탐색 트리의 특성 때문이다.
만약 후계자 노드가 왼쪽 서브트리에서 가장 작은 노드가 오면 어떻게 될까?

위의 트리에서 8 노드를 삭제하려고 한다.
그렇다면 왼쪽 서브트리에서 가장 작은 노드는 1이 될 것이다.
만약 1이 올 경우 트리는 아래와 같이 변경된다.

1이 오게 되면 왼쪽 자식 노드는 부모 노드보다 작다는 성질을 위반하게 된다.
쉽게 생각해서 삭제하고자 하는 노드의 왼쪽 서브트리의 가장 큰 노드와 오른쪽 서브트리의 가장 작은 노드는 삭제되는 노드와 가장 비슷한 노드일 것이다.
그렇기 때문에 이 노드들이 후계자 노드가 되는 것이다.

만약 8 노드를 삭제하는 경우, 후계자 노드는 왼쪽 서브트리에서 가장 큰 수인 7, 오른쪽 서브트리에서 가장 작은 수인 9가 된다.
- 후계자 노드가 7인 경우
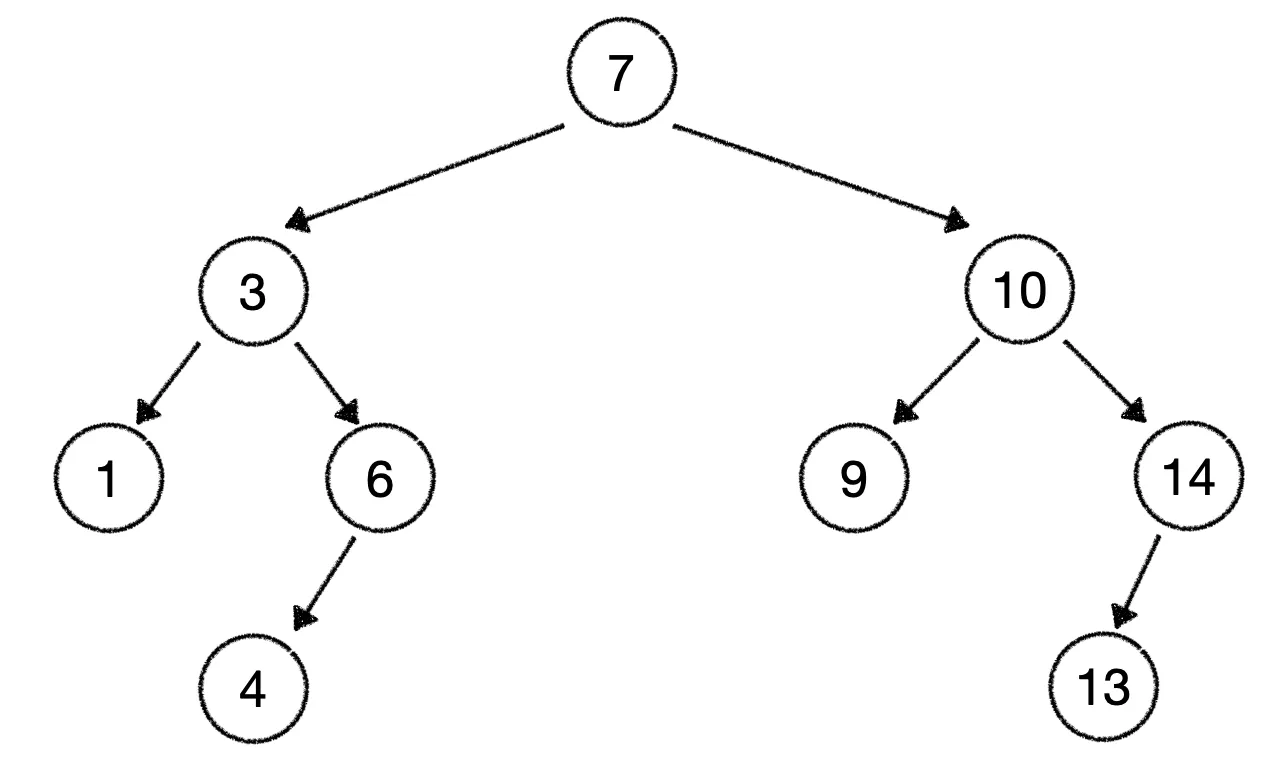
- 후계자 노드가 9인 경우

보다시피 두 트리 모두 이진 탐색 트리의 형태를 유지한다.
자식이 있는 노드를 삭제하는 경우
아래 이미지는 14 노드를 삭제하는 경우이다.

14 노드의 후계자 노드는 13이 된다. (오른쪽 서브트리는 없으므로 탐색 X)

만약 자식 노드의 수가 2개인 10 노드를 삭제하는 경우는 아래와 같다.
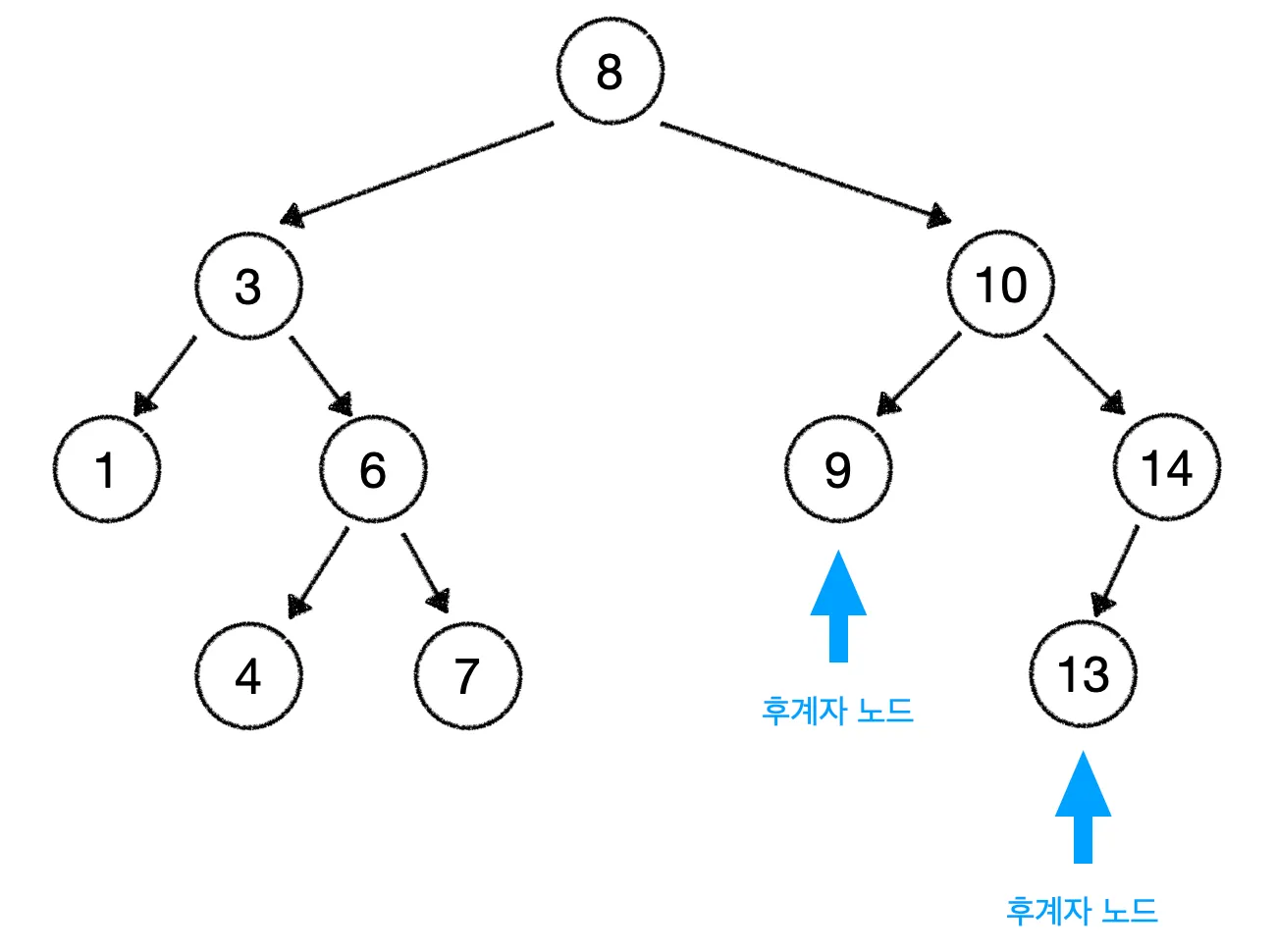
왼쪽 서브트리의 가장 큰 노드인 9, 오른쪽 서브트리의 가장 작은 노드인 13이 후계자 노드가 된다.
둘 중 아무거나 10 노드의 위치에 있어도 된다.
느낀 점
자료구조를 이렇게 깊게 공부한 게 상당히 오랜만이다..
다음번엔 B-Tree, B+Tree도 깊게 공부해야지..
'개발 일기' 카테고리의 다른 글
| [개발 일기] 2025.01.16 - B+Tree (0) | 2025.01.16 |
|---|---|
| [개발 일기] 2025.01.15 - B-Tree (0) | 2025.01.15 |
| [개발 일기] 2025.01.13 - com, kr, co.kr 등등 이 나눠져있는 이유? (Feat : 최상위 도메인) (1) | 2025.01.13 |
| [개발 일기] 2025.01.12 - OSI 7계층 (응용 계층) (0) | 2025.01.12 |
| [개발 일기] 2025.01.11 - OSI 7계층 (표현 계층) (0) | 2025.01.11 |