개요
코딩테스트를 볼 때 이분탐색을 사용하는 문제는 심심치 않게 나온다.
그리고 이러한 이분 탐색의 세부 알고리즘으로 하한선(Lower Bound)과 상한선(Upper Bound)으로 나뉜다.
오늘은 이 두 알고리즘에 대해 정리해보자.
Lower Bound
하한선은 목푯 값 이상인 첫 번째 위치를 찾는 탐색이다.
배열에서 목표 값 이상이 시작되는 가장 작은 인덱스를 반환한다.
쉽게 말하면 목표 값의 시작 위치를 찾는 알고리즘이다.
Lower Bound 동작 방식
1. 첫 번째로 left는 찾고자 하는 값이 들어있는 배열의 왼쪽 끝, right는 오른쪽 끝에서 시작한다.
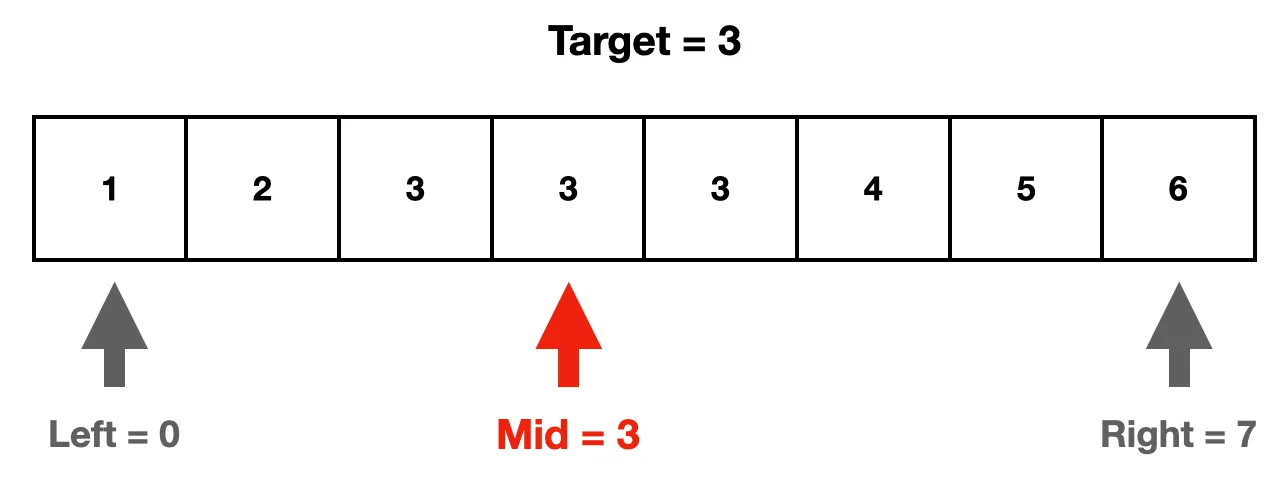
2. left와 right의 중간 인덱스를 나타내는 mid((left + right) / 2)를 계산한다. 만약 arr [mid]의 값이 target보다 크거나 같으면 right 인덱스를 mid 인덱스로 옮긴다.

3. right를 mid가 있던 인덱스로 옮긴 후, 다시 1번 과정을 반복한다.
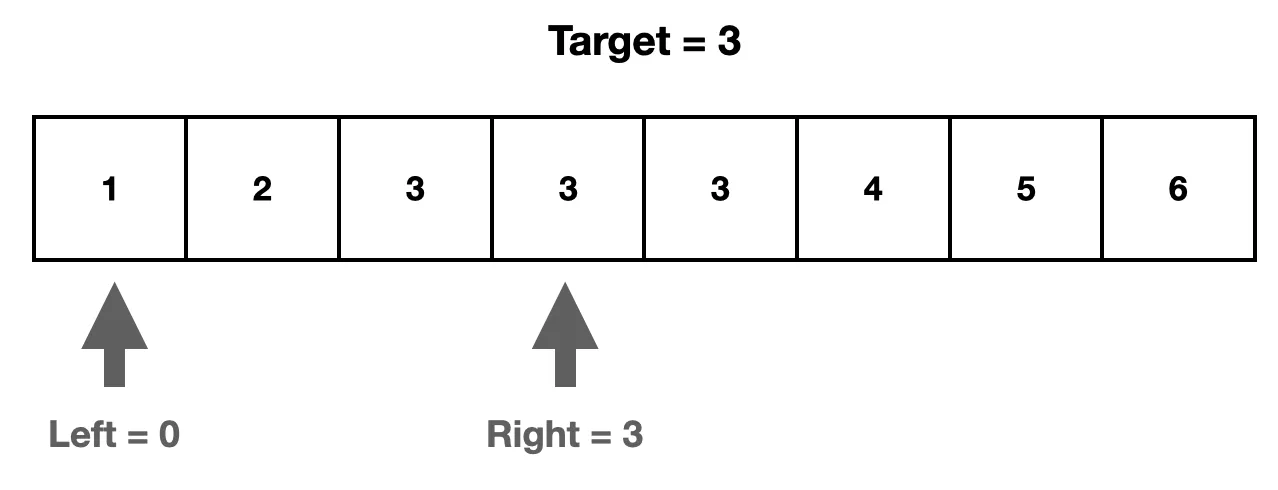
4. arr [mid]의 값이 target보다 작은 경우, left를 mid+1 인덱스로 옮긴다.그 이유는 우리가 찾고자 하는 인덱스는 target 이상의 값이 시작되는 인덱스이다. 만약 arr[mid]의 값이 target보다 작다면 mid이전의 모든 값들은 탐색할 필요가 없기 때문이다.


5. mid을 계산한 후, arr[mid]의 값을 확인한다. 확인한 결과, arr [mid]는 target 이상이다. 그러므로 right를 mid로 옮긴다.


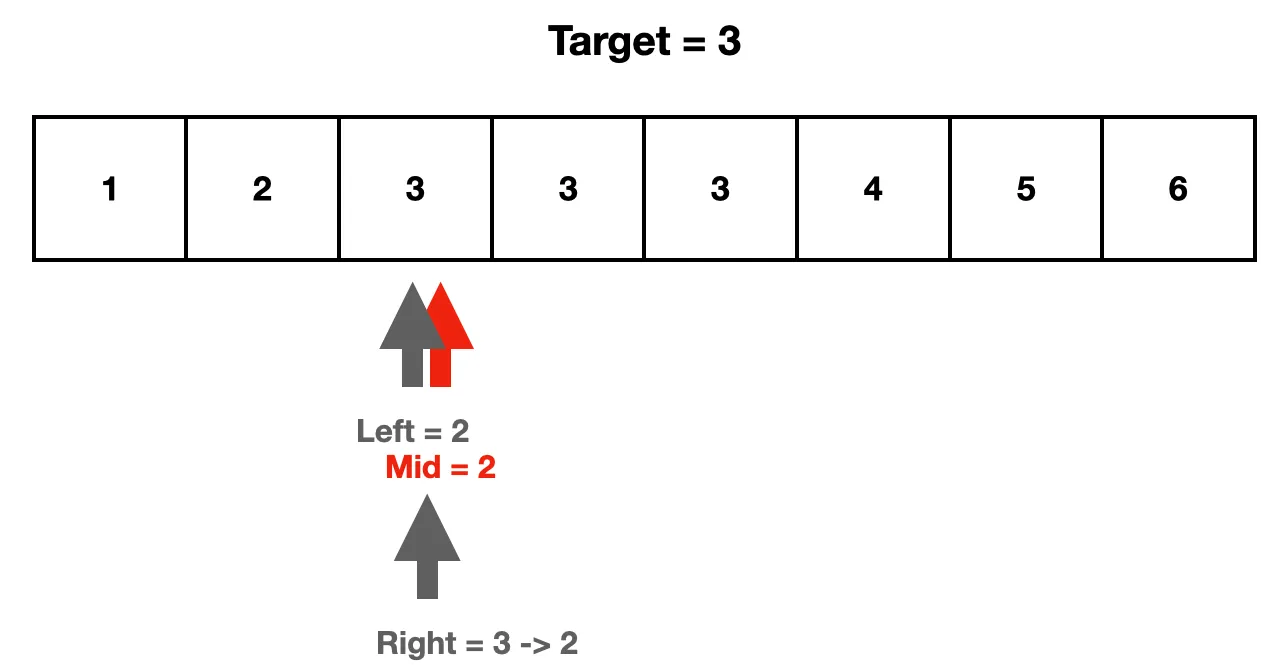
6. right를 mid로 옮긴 후, left와 right를 비교하니 서로 같다. 이후 while(left < right) 조건문에 의해 반복문에서 탈출한다.

Lower Bound 예시 코드
public static int lowerBound(int[] arr, int target) {
int left = 0, right = arr.length;
while (left < right) {
int mid = (left + right) / 2;
if (arr[mid] >= target) {
high = mid; // 목표 값 이상이 시작되는 위치를 탐색
} else {
left = mid + 1;
}
}
return left; // 목표 값 이상인 첫 번째 위치 반환
}
참고로 left를 반환하는 이유는 우리가 찾고자 하는 값이 target 이상의 값이 처음으로 등장하는 인덱스이기 때문이다.
그리고 위의 코드를 보다시피 left는 절대 target보다 작을 수 없다. (left = mid + 1)
right의 역할은 탐색 범위를 줄이는 역할만 담당한다.
Upper Bound
상한선은 목푯 값 초과인 첫 번째 위치를 찾는 탐색이다.
배열에서 목표 값 초과가 시작되는 가장 작은 인덱스를 반환한다.
쉽게 말하면 목표 값보다 큰 값의 시작 위치를 찾는 알고리즘이다.
Upper Bound 동작 방식
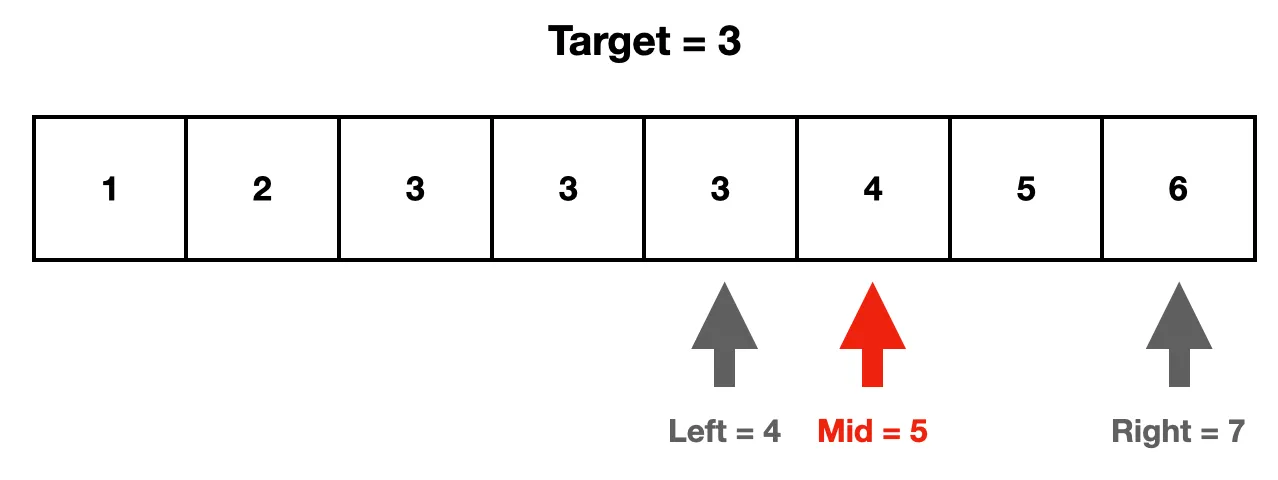
1. 첫 번째로 left는 찾고자 하는 값이 들어있는 배열의 왼쪽 끝, right는 오른쪽 끝에서 시작한다.
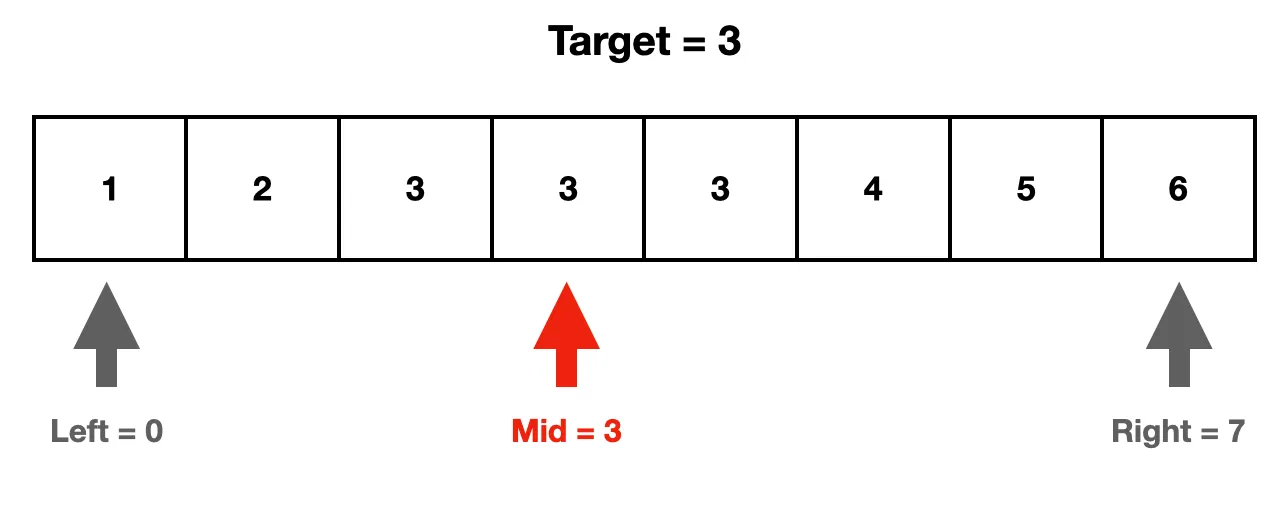
2. arr [mid]의 값이 target과 같다. 우리가 찾고자 하는 값은 target을 초과하는 값을 가진 인덱스이다. 그러므로 mid 이전 인덱스 모두를 탐색 범위에서 제외하기 위해 left를 mid+1로 옮긴다.

3. arr [mid]가 target을 초과한다.그 의미는 arr[mid]가 우리가 찾고자 하는 target을 최초로 초과하는 인덱스가 될 수 있다는 것이다. 그러므로 범위를 줄이는 용도인 right를 mid로 옮긴다. 그 이유는 left와 mid 사이의 인덱스가 우리가 찾고자 하는 인덱스이기 때문이다.
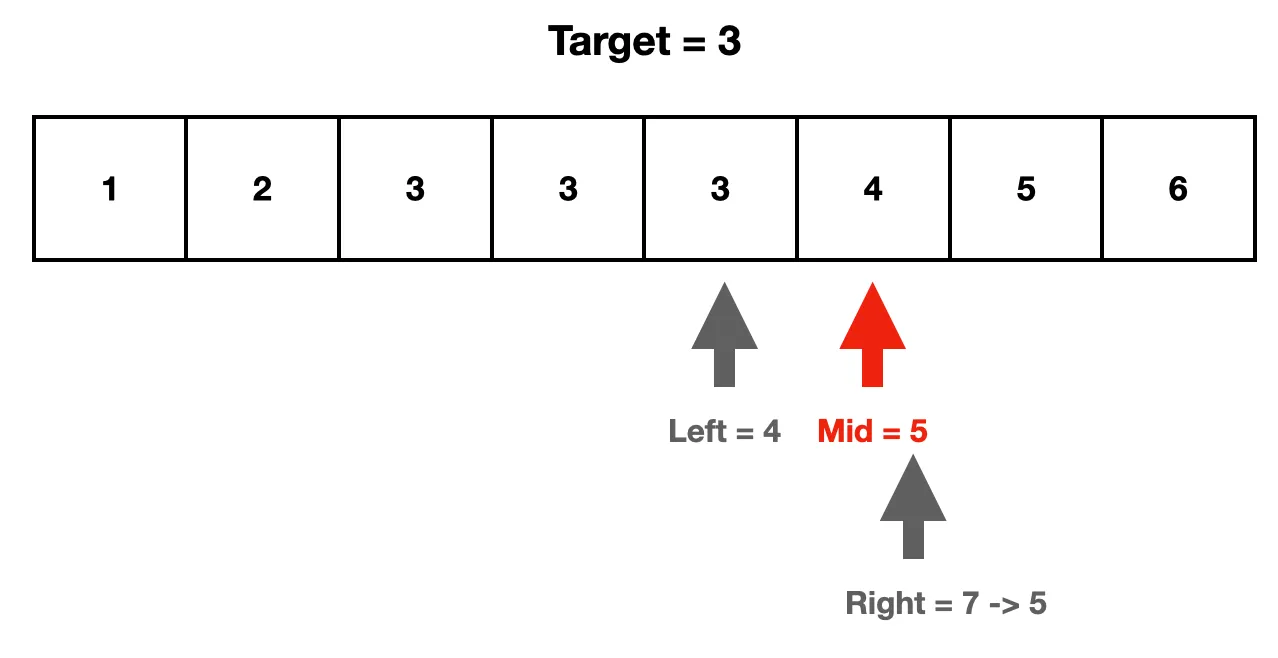
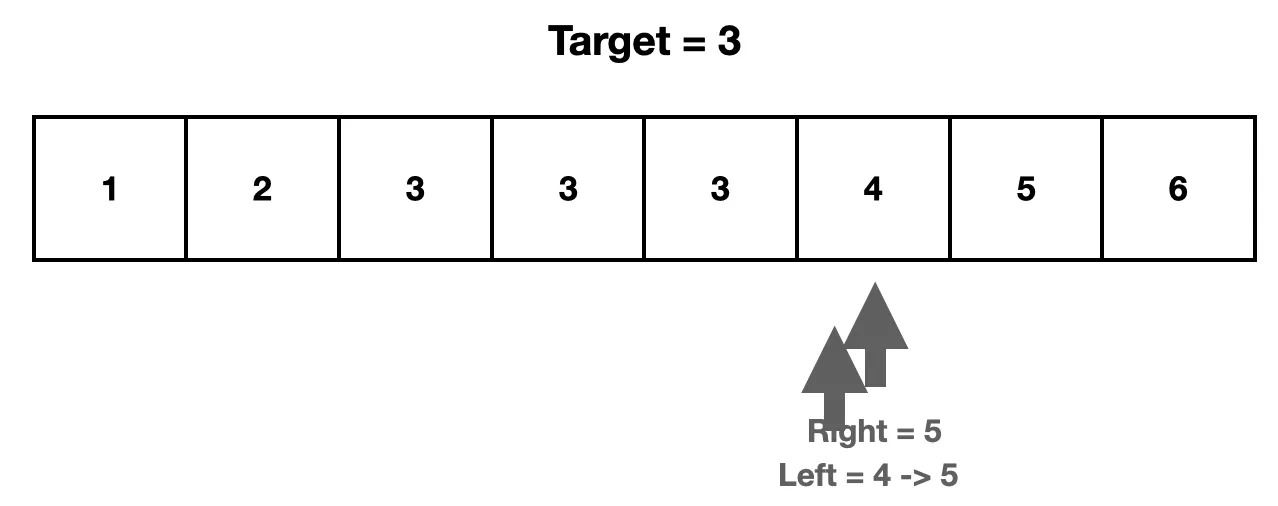
4. arr [mid]의 값이 target과 같다. 그러므로 mid 이전의 인덱스를 탐색 범위에서 제한하기 위해 left를 mid+1로 옮긴다.

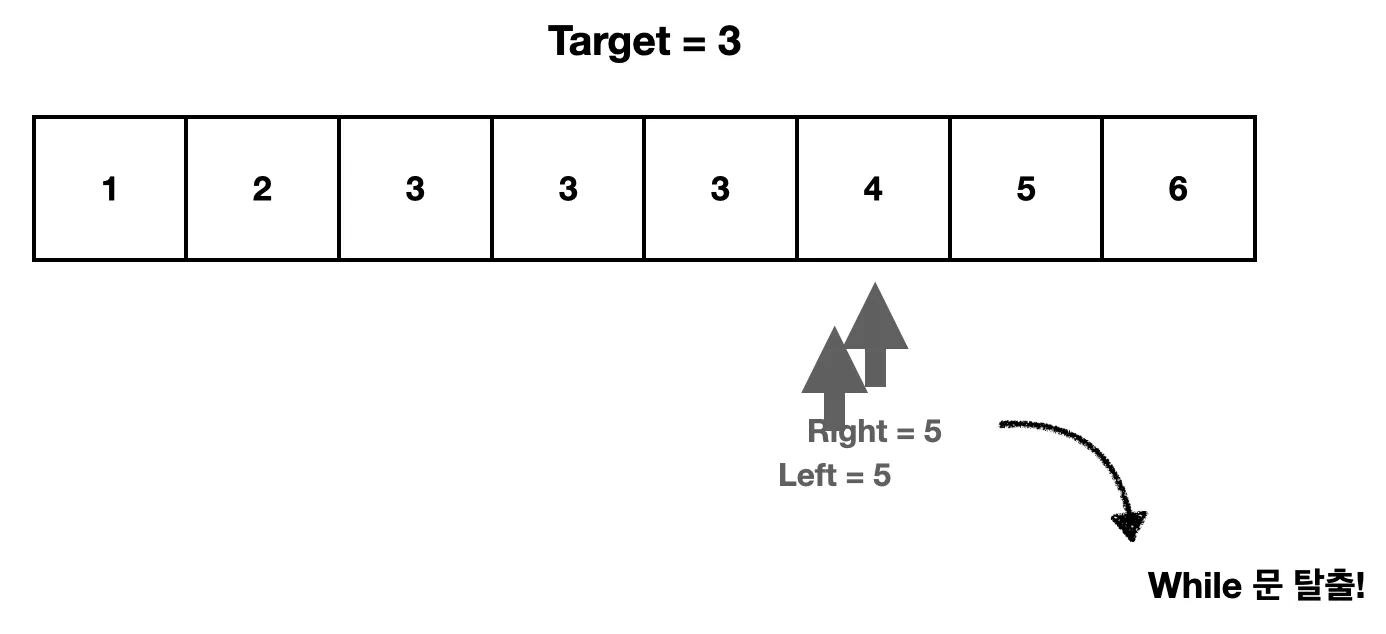
5. 옮긴 후, while (left < right) 조건에 걸리게 되어 반복문이 종료된다.
Upper Bound 예시 코드
public static int upperBound(int[] arr, int target) {
int left = 0, right = arr.length;
while (left < right) {
int mid = (left + right) / 2;
if (arr[mid] > target) {
right = mid; // 목표 값 초과가 시작되는 위치를 탐색
} else {
left = mid + 1;
}
}
return left; // 목표 값 초과인 첫 번째 위치 반환
}
이분탐색의 까다로운 점
이분탐색의 가장 까다로운 점은 다음과 같다.
- while (left < right) vs while (left ≤ right)
- return left vs return right
난 아직까지도 알고리즘을 풀 때 이러한 문제 때문에 골치가 아프다.
이러한 고민을 ChatGPT에게 물어본 결과, 다음과 같은 답변을 받았다.
| 조건 | left < right | left <= right |
| 탐색 범위 | [left, right) (반열린 구간) | [left, right] (닫힌 구간) |
| 종료 조건 | left == right | left > right |
| 적합한 상황 | 특정 위치(삽입 위치 등)를 찾는 경우 | 정확히 특정 값을 찾는 경우 |
| 사용 사례 | Lower Bound, Upper Bound 문제 | 일반적인 이분 탐색 |
| 조건 | return left | return right |
| 탐색 범위 | [left, right) (반열린 구간) | [left, right] (닫힌 구간) |
| 종료 조건 | left == right | left > right |
| 적합한 상황 | 특정 위치(삽입 위치 등)를 찾는 경우 | 정확히 특정 값을 찾는 경우 |
| 사용 사례 | Lower Bound, Upper Bound 문제 | 일반적인 이분 탐색 |
탐색 범위가 [left, right)이면 return left
탐색 범위가 [left, right]이면 return right
고마워요 챗지피티!
'개발 일기' 카테고리의 다른 글
| [개발 일기] 2025.01.30 - 객체 지향 생활 체조 9가지 규칙 (1) (0) | 2025.01.30 |
|---|---|
| [개발 일기] 2025.01.29 - 불변 객체 (0) | 2025.01.29 |
| [개발 일기] 2025.01.27 - Nginx (Feat : Apache Web Server) (0) | 2025.01.27 |
| [개발 일기] 2025.01.26 - 논리적 동치성 (Feat : equals()) (1) | 2025.01.26 |
| [개발 일기] 2025.01.25 - volatile (1) | 2025.01.25 |